(Ciencias
de Joseleg)(Química)(La materia)(La materia y sus propiedades)(Ejercicios resueltos)(
Introducción a la
materia)( Que es la química)(
Historia de la
química)( Los modelos
científicos)( Los métodos
científicos)( Los estados de la
materia)( Tipos de propiedades
de la materia)( Introducción a las
unidades y medidas)( Sustancias puras e
impuras)( Elementos y
compuestos)(Abundancia de los
elementos)( Introducción a la
energía química)( Referencias
bibliográficas)
En esta sección
haremos una introducción somera de las unidades y medidas, pues se espera que
este concepto se examine con mayor profundidad en su curso de física. Las
unidades de medición son magnitudes definidas con base a la comparación con un
patrón, definido y adoptado por arbitrio de un grupo de personas, que luego es
empleada como estándar para medir otras magnitudes en términos de cuantas veces
se repite la cantidad patrón. Por ejemplo, la gente hace mucho tiempo se puso
de acuerdo en que un cilindro de un metal especial se llamaría EL KILOGRAMO,
luego las mediciones de todas las demás masas en el mundo se establecieron por
mucho tiempo (hasta 2019) comparándolas con copias de ese KILOGRAMO.
En ese orden de
ideas, los científicos deben ponerse de acuerdo en unas pocas propiedades
cuantitativas básicas, y luego ponerse de acuerdo en cómo crear el patrón de
medición para comparar. El conjunto de acuerdos sobre la medición es un sistema
de unidades y medidas, y en ciencia usamos únicamente el denominado Sistema
Internacional.
Las propiedades cuantitativas tienen los siguientes componentes:
| Ecuación 01. |
Donde (m) representa el símbolo de la magnitud
física medida, en este caso la masa. Las magnitudes siempre están asociadas a
un objeto que es medido, si se desconoce el objeto entonces entre paréntesis o
como subíndice se coloca una (i) u otro
símbolo, pero si se conoce el objeto se usa su nombre o un símbolo que lo
represente, en nuestro caso el nombre de la persona (JOSE).
El valor, que en
este caso es (74) representa la cantidad de veces que se repite el patrón en el
objeto medido, en este caso implica que José equivale a 74 cilindros del
kilogramo patrón usado antes de 2019.
Las unidades (kg)
representa el nombre de la unidad patrón, la cual puede ser un símbolo básico o
un símbolo compuesto. Tenga en cuenta que una magnitud solo puede tener un
conjunto de unidades asociadas, por ejemplo, una masa no puede expresarse en
unidades de velocidad. Tenga en cuenta que, en este curso de química, los
símbolos de las magnitudes físicas o propiedades cuantitativas serán expresadas
en cursiva, mientras que los símbolos de las unidades estarán escritos en texto
normal.
Las siete unidades
base y su respectiva dimensión son: Distancia medida en metros; Masa medida en
kilogramos; Tiempo medido en segundos; Corriente eléctrica medida en amperios;
temperatura medida en Kelvin; Intensidad lumínica medida en candelas; cantidad
de sustancia medida en moles.
Tabla 1. Las siete magnitudes y unidades fundamentales y sus símbolos.
Las 7 unidades base
se definen de ser posible en base a criterios físicos inmutables, que
teóricamente deben comportarse igual en cualquier parte del universo que no sea
un horizonte de sucesos “un agujero negro”, en otras palabras, dichas
definiciones deben intentar ser extraíbles de fenómenos generales.
El 16 de noviembre
de 2018, la 26ª Conferencia General sobre Pesos y Medidas (CGPM) votó por
unanimidad a favor de la revisión de las definiciones de las unidades base del
SI, que el Comité Internacional de Pesos y Medidas (CIPM) había propuesto
anteriormente. Las nuevas definiciones entrarán en vigor el 20 de mayo de 2019.
El kilogramo, el amperio, el kelvin y el mol se definirán estableciendo valores
numéricos exactos para la constante de Planck (h), la carga eléctrica elemental (e), la constante de Boltzmann (k)
y la constante de Avogadro (NA),
respectivamente. El metro y la candela ya están definidos por constantes
físicas, sujetas a corrección a sus definiciones actuales únicamente por
mejoras tecnológicas. Las nuevas definiciones apuntan a mejorar el SI sin
cambiar el tamaño de las unidades, asegurando así la continuidad con las
mediciones existentes de 2019 (Esser, 2018;
NIST, 2018).
Lo anterior implica
que todos los libros de texto escritos antes de 2019 que definen al kilogramo
como el cilindro de metales especiales quedaron obsoletos, pero en términos
prácticos, la nueva definición solo afecta en mediciones científicas de
ultra-alta exactitud, recuerde que una redefinición de una unidad de medida se
calcula de forma tal que altere lo menos posible las unidades que están en
vigor para usos menos precisos, pero es bueno tener en cuenta que el kilogramo
ahora puede medirse sin tener en cuenta un cilindro específico almacenado en
una bóveda específica, de una ciudad específica de un país específico.
A partir de las
unidades fundamentales se derivan las unidades de medida de todas las otras
magnitudes o propiedades cuantitativas, las cuales iremos introduciendo
paulatinamente en este curso.
Tal como se empleaba
en el primer sistema métrico decimal, se emplean prefijos griegos para las
medidas largas, más grandes que la unidad base; y prefijos derivados del latin
para las medidas cortas que son más pequeñas que la unidad base. Cada prefijo
va asociado a una determinada potencia de 10, aunque su uso se hará claro
cuando introduzcamos el concepto de notación científica y factor de conversión.
Por lo general la
unidad base, su realización física y su expresión matemática son iguales,
excepto para la unidad de masa, el kilogramo. En este la unidad base y la
realización física concuerdan, pero su uso matemático no, para la matemática de
la masa emplearemos como unidad base el gramo, y sobre él es que realizaremos
las modificaciones con los prefijos. Cuando elevamos cualquier número al
exponente 0, el resultado es igual a 1, por eso podemos multiplicar cualquier
número por (100) y el resultado será exactamente el mismo número
original (BIPM, 2006).
Gramática de las unidades y medidas
Los nombres de las
unidades se expresan como sustantivos comunes, lo cual implica que deben ser
escritos con letras minúsculas aun cuando dichos nombres sean honoríficos a
grandes científicos. De esta forma cuando escribimos Newton con mayúscula
hacemos referencia al apellido de Isaac Newton el célebre científico, pero
cuando escribimos newton con minúscula estamos hablando de las unidades de
fuerza básicas. Para las unidades que están asociados al símbolo grado se
expresa el nombre, ya sea grados a secas cuyo símbolo es (°) o grados
centígrados (°C), sin embargo, kelvin en la actualidad ya no se escribe
antecediendo el grado.
Como tal la
pronunciación y nombre de cada unidad puede adaptarse a las convenciones
locales de cada idioma, por ejemplo, el litro puede escribirse como liter
o litre
dependiendo de su idioma. Por otra parte, cuando aplicamos la pluralidad, por
ejemplo, varios metros aplicamos las reglas locales de cada idioma para convertir
el sustantivo en plural, en español esto se logra agregando la (s) al final en
la mayoría de los casos.
Si nos encontramos
con decisiones difíciles como el Newton, entonces aplicaremos lo siguiente.
Los nombres con final consonante procedentes de lenguas extranjeras y no
enteramente aclimatados forman el plural con una -s
añadida directamente a la consonante final: salacot, salacots;
complot, complots... Los terminados en -r, de adopción más fácil, forman
normalmente el plural en -es: bar, bares; yogur, yogures. Por lo que el
plural para newton será newtons. Para el caso de Hertz que también es una
decisión difícil empleamos el sinónimo singular hercio y el plural será
hercios. El problema es que nos podemos encontrar con otros casos molestos.
A pesar de que el
nombre de las unidades es dependiente del idioma local, la escritura de las
unidades y sus magnitudes debe ser consistente en todo el mundo, de lo
contrario el tratado del metro no serviría para nada. Idealmente las siguientes
reglas deben aplicar para productos formales en procesadores de texto o en
escritos a mano, pero el hecho de que a mí nunca me los hubiera enseñando
implica que a muchos les importa un comino. En cualquier caso, es conveniente
tratar de usar estas reglas.
· El valor de la magnitud es seguido por un
espacio que representa el signo de multiplicación y luego se coloca el símbolo
de la unidad, por ejemplo 70 kg, 7,3 m, 22 K. Esta regla también incluye el
símbolo porcentual (%), pero no a los símbolos de medida de arcos ya sean
grados, arcos minutos o arcos segundos (°, ′, ″) en los cuales no se deja
espacio.
· Los símbolos son términos algebraicos no
siglas, por lo que no se les agrega punto final, a menos que sea el fin de una
oración o un párrafo.
· Los prefijos decimales hacen parte de la
unidad, esto implica que no se le deja espacio con respecto al símbolo base, y
se trata como un todo individual por ejemplo k en km, M en MPa o G en GHz. No
se permiten prefijos compuestos.
· Si expresamos un compuesto generado por una
unidad derivada se debe emplear un punto central o un espacio para no
confundirse con un símbolo decimal por ejemplo N m o N·m.
· Los símbolos de unidades derivadas que
implican divisiones se representan con el / o con exponente negativo. Por
ejemplo (m/s = m s-1 = m·s-1).
· Con respecto a la regla anterior, si estamos
escribiendo en renglón como en Word o en un blog debe evitarse colocar más de
un / pues eso es confuso, por lo que se aconseja dominar la notación de
potencia negativa.
· Si el símbolo deriva del apellido de un
científico célebre, dicho símbolo se escribe en mayúscula, o si tiene más de
una letra, la primera en mayúscula y las demás en minúscula, por ejemplo, el
pascal (Pa) en honor de Blaise Pascal. La única excepción es el litro que lo
pueden escribir como se les dé la gana, ambas son aceptables, pero por
costumbre usamos (L) mayúscula cuando no está acompañado de un prefijo decimal,
y empleamos (l) minúscula cuando si lo está como en mililitros (ml). La
recomendación sin embargo es que se escriba la (L) mayúscula para que no se
confunda con el uno.
· Los símbolos jamás se expresan pluralmente,
por ejemplo 25 kg se pronuncia kilogramos, pero el símbolo jamás se escribe
como kgs ya que genera confusiones con el símbolo de la unidad de tiempo, el
segundo (s).
· Las mayúsculas y minúsculas tienen
significado, por lo que es estrictamente obligatorio escribirlos según las
recomendaciones de las listas, por ejemplo, los valores mW y MW difieren en
enormes órdenes de magnitud y en consecuencia no son intercambiables. La
primera unidad miliwatt (mW) es la potencia típica de un audífono, mientras que
megawatt (MW) representa la potencia necesaria para mover un tren. Es
importante para aquellos que solo escriben sus textos en mayúsculas.
· El separador decimal puede ser un punto (.) o
una coma (,). En la practica el punto es empleado en los países angloparlantes,
Méjico y en Asia, mientras que la coma es empleada en la zona europea y
Latinoamérica con algunas excepciones. Sea cual sea la elección, debe mantenerse
la consistencia.
· Para separar los tres ceros con valor a la
derecha se emplea un espacio en lugar de puntos o tildes, para evitar
confusiones.
· Debido a que las definiciones de billón y
trillón difieren de un idioma a otro, las pseudounidades de partes por millón y
partes por trillón deben ser descontinuadas.
· En un procesador de texto los símbolos de
magnitud y los símbolos de unidad deben poder identificarse. Las unidades se
escribirán en fuente simple (m, s, kg, A), y los símbolos de magnitudes se
escribirán en cursivas o con un tipo de texto que sea semejante al itálico (x, t, m, I).
La notación
científica es un modo de expresar muy grandes o muy pequeñas cantidades de
manera corta y aproximada, así como la expresión alternativa de los prefijos
decimales del Sistema Internacional de Unidades. Básicamente se basa en el
manejo de las potencias con base 10.
Generalmente, muchos estudiantes tienen problemas con poder controlar
las potencias de 10 y sus operaciones, y es por esta razón que le dedicaremos
cierta atención a este tema.
La notación
científica es una manera de escribir números que son muy extensos. Para hacer
esto se hace uso de las reglas de los exponentes, en concreto de los exponentes
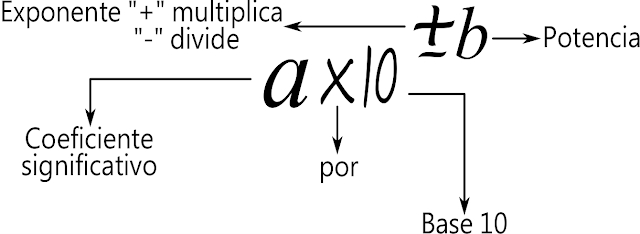
de base 10. Un número expresado
científicamente está compuesto por una o más cifras significativas multiplicado
por una o base 10 elevada a un determinado exponente, este exponente indica la
cantidad de ceros a la derecha o a la izquierda de la cifra significativa.
Coeficiente significativo
Todos los dígitos
que aparecen a la izquierda del signo de multiplicación “X” son significativos,
aun cuando sean ceros.
Si el exponente de
la notación científica es positivo, estamos tratando con ceros a la derecha de
las cifras significativas y por lo tanto de un número muy grande.
Si el exponente de
la notación científica es negativo, estamos tratando con ceros a la izquierda de
las cifras significativas y por lo tanto de un número muy pequeño.
La cantidad de cifras significativas, la posición de la coma y el exponente se encuentran directamente relacionados. Alterar la posición de la coma involucra necesariamente alterar el exponente. Esto es particularmente útil cuando el coeficiente significativo no es un entero. Mover la coma a la derecha disminuye el exponente, y mover la coma a la izquierda aumenta el exponente.
Para sumar o restar
dos números expresados como notación científica, se debe fijar en el exponente
primero y luego en las cifras significativas. La regla nos dice que sólo se
puede sumar o restar cifras significativas cuyos exponentes sean iguales, de lo
contrario se deben igualar los exponentes alterando la cantidad de cifras
significativas en uno de los valores a sumar o restar.
La multiplicación de
notaciones científicas sigue la regla de sumar ceros o de sumar la potencia,
esto se puede hacer debido a que la base es la misma. A diferencia de la suma o
la resta, la multiplicación puede hacerse con cualquier potencia, por lo que
los factores no necesariamente deben tener la misma potencia.
Con la multiplicación vamos a ejecutar un paso intermedio que involucra aplicar la ley conmutativa de la multiplicación. Dado que el orden de los factores no altera el producto, colocaremos los dos coeficientes a un lado y las dos potencias al otro. Multiplicamos aritméticamente los coeficientes, mientras que la multiplicación de las potencias es dejar la base 10 y sumar los exponentes.
Un valor en notación
científica elevado a una potencia puede gozar de la ley conmutativa, el
coeficiente se opera de forma independiente, mientras que el exponente se
multiplica por tantas veces indique la potenciación.
Cuando realizas una
medida, empleas algún tipo de instrumento de medición. Por ejemplo, pues
emplear metro para medir una altura, una balanza para determinar un peso, a un
termómetro para determinar una temperatura. Por lo general los valores medidos
directamente deben ser empleados in cálculos matemáticos que no siempre arrojan
números enteros. Para poder controlar la cantidad de decimales obtenidos en
dichos cálculos se emplea una serie de reglas que se denominan en su conjunto
como cifras significativas. Las cifras significativas son una serie de valores
que portan un significado verdadero al interior del número. Antes de aprender a
operar empleando las cifras significativas, es esencial aprender a reconocerlas
en diferentes tipos de números.
Todos los números
enteros son cifras significativas, aunque sean ceros, por ejemplo, el numero 50
poseen dos cifras significativas, el 100 posee tres cifras significativas, el
1000 posee cuatro cifras significativas y así sucesivamente. Esto se cumple a
menos que sea el resultado de una operación, pues de ser así muchos de esos
ceros no son significativos y hay que aplicar las siguientes reglas.
Los ceros
intermedios cuentan como cifra significativa, no solo cuando hacen parte de un
entero como en 101 o en 208, sino también cuando hacen parte de una expresión
decimal. Por ejemplo 5,008 posee cuatro cifras significativas.
Si hacen parte de un
entero siempre son significativos, si se encuentran a la derecha de una coma
solo son significativos si el contexto o del problema o del ejercicio o así lo
determinan.
Aunque las
notaciones científicas expresan valores enteros muy grandes, o una enorme
cantidad y se los intermedios, generalmente se asume como con significado solo
los valores diferentes de cero que se expresan a la izquierda la notación, por
ejemplo, en 6,022 x 1023 se tiene un valor entero enorme, pero con
significado sólo hay cuatro valores. Las siguientes reglas están relacionadas
con la presente.
Cuando están
presentes muchos ceros a la izquierda, éstos carecen del significado por
ejemplo 0,0003 solo tiene una cifra significativa. La definición de muchos es
ambigua en este caso, la mejor guía es si se trata de un dato o del resultado
de una operación matemática. Si se trata de un dato el valor se toma con todos
sus números significantes, pero si el valor es resultado de una operación, los
ceros a la izquierda se dividirán como con significado o sin significado según
las reglas de operación que veremos posteriormente.
Cuando están
presentes muchos ceros a la derecha, esos carecen de significado por ejemplo
1000 sólo tendría una cifra significativa. La definición de muchos es ambigua
en este caso, la mejor guía es si se trata de un dato o del resultado de una
operación matemática. Si se trata de un dato el valor se toma con todos sus
números significantes, pero si el valor es resultado de una operación, los
ceros a la derecha se dividirán como con significado o sin significado según
las reglas de operación que veremos posteriormente.
Tenga en cuenta que
valores como 1000 puede tener una o cuatro cifras significativas, la
determinación de esto va a defender enteramente del contexto del problema o el
ejercicio que se esté trabajando. Básicamente la guía es si se trata de un dato
o si se trata del resultado de una operación.
Para el caso de las
evaluaciones de estado, las cifras significativas estarán dictadas por las
opciones de respuesta.
Cuando eliminadas
las cifras decimales para obtener las cifras significativas, te ves obligado a
realizar la operación de redondeo. La regla redondeo es la siguiente, se tiene
que identificar la primer cifras sin significado a la derecha, si esta cifra es
4 o menos entonces escribe el número hasta la última cifra significativa sin
alterarlo; si y la cifra no significativa es igual a 5 o más entonces la
primera cifra significativa aumenta en una unidad.
En sumas y restas
las cifras significativas de la respuesta dependen de la cantidad de decimales,
la respuesta tendrá la misma cantidad de decimales que el sumando con menos
decimales (4,54 + 3,3 = 7,8).
Para
multiplicaciones y divisiones las cifras significativas de la respuesta serán
iguales a las cifras significativas del término medido con menos cifras
significativas.
Las constantes
universales no se toman en cuenta para determinar las cifras significativas.



No hay comentarios:
Publicar un comentario