[Ciencias de Joseleg]
[Química]
[La
materia] [Química
de gases] [Ejercicios
resueltos] [Introducción]
[Generalidades]
[Propiedades
de los gases] [Temperatura]
[Volumen]
[Presión]
[Masa
y moles] [Historia]
[La
ley de Boyle] [La
ley de Charles] [La
ley de Gay-Lussac] [Ley
de volúmenes de combinación] [Las
leyes de Avogadro] [Ley
de los gases ideales PV=nRT] [Modificaciones
a PV=nRT] [Ley
de Dalton de presiones] [Estequiometría
de gases] [Concentración
de un gas] [Gases
húmedos] [Ley
de los gases reales] [Ejercicios
especiales] [Referencias
bibliográficas]
La presión (P) es la fuerza F aplicada perpendicularmente a la superficie A de un objeto por unidad de área sobre la cual se distribuye esa fuerza. El desarrollo del concepto de presión estuvo vinculado a la discusión sobre la existencia del aire como sustancia que ocupa un lugar en el espacio. Normalmente no podemos calcular la presión directamente ya que no medimos todas las fuerzas con dinamómetros, en su lugar empleamos la masa.
🔎
DEMOSTRACION. Demuestre
una función que permita calcular la presión en función de la masa de un objeto,
la gravedad del planeta y el área.
La ecuación anterior nos permitirá
resolver situaciones como:
✔ Ejercicio 10.15. Suponga que una mujer que
pesa 130 lb y usa zapatos de tacón alto momentáneamente coloca todo su peso
sobre el talón de un pie. Si el área del talón es de 0.50 pulg2,
calcule la presión ejercida sobre la superficie subyacente en (a) kilopascales,
(b) atmósferas y (c) libras por pulgada cuadrada.
✔ Ejercicio 10.16. Un conjunto de estantes para libros descansa
sobre una superficie de piso duro sobre cuatro patas, cada una con una
dimensión de sección transversal de 3.0 x 4.1 cm en contacto con el piso. La
masa total de los estantes más los libros apilados en ellos es de 262 kg.
Calcule la presión en pascales que ejercen las zapatas sobre la superficie.
La existencia del aire
¿Cómo sabemos que el aire existe y pesa?
La existencia del aire es algo evidente cuando este fluye de un lugar a otro
formando el viento, pero lo que es menos evidente es que esa cosa, sea lo que
fuere, tiene un peso asociado y ocupa un lugar en el espacio. Existe una sutil
diferencia entre darse cuenta de que el aire es una sustancia (en oposición a
un vacío), establecer que tiene peso y luego intentar medir dicho valor.
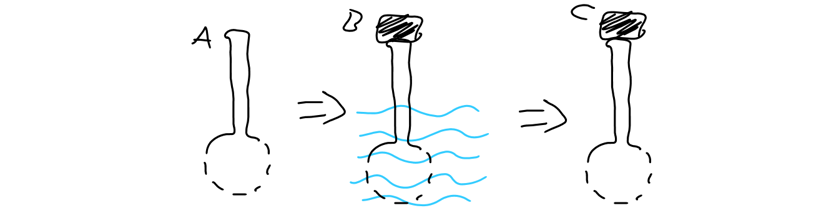
Figura 6‑1. Una clepsidra (A) es en esencia una cabeza de ducha, pero sin una
tubería de apoyo, para llenarla debes sumergir la cabeza en agua y poner tu
dedo en el orificio (B), cuando se la retira del agua, esta retiene líquido
siempre y cuando el orificio opuesto esté tapado (C). Si se retira el dedo,
entonces el agua sale.
Si se sumerge una clepsidra, el agua ingresará, y si esta se retira, el agua saldrá por los múltiples orificios formando muchos chorros individuales, semejantes a las cabezas de un dragón de muchas cabezas, de allí que el aparato comparta el nombre la raíz de su nombre con la Hidra de Lerna. Lo interesante es que, si se pone el dedo en el tubo opuesto a la cabeza de la clepsidra, y se retira esta del pozo, no perderá agua de manera significativa, aunque los orificios pequeños estén abiertos, pero al momento de retirar el dedo, los orificios de la cabeza comenzarán a emitir sus chorros de agua.
Figura 6‑2. Si el orificio superior está obstruido la única presión que se
ejerce es sobre los orificios inferiores hacia arriba , lo cual evita que el
agua se mueva, siempre y cuando la presión en cada orificio sea inferior a la
presión que ejerce la atmósfera. Si el orificio superior se abre, la presión
atmosférica ejercerá fuerza desde arriba y desde abajo cancelándose, y
permitiendo el flujo de agua.
Sin embargo, si el extremo está cubierto
con su dedo mientras se sumerge la cabeza en el pozo no entra agua por los
huecos, ni sale aire tampoco, esto demostró que el aire y el agua son
sustancias que pueden llenar un mismo espacio, pero no de manera simultánea, si
una ingresa, la otra sale, por lo tanto, no puede entrar agua hasta que sale el
aire, ergo el aire es una sustancia y no un espacio vacío.
Figura 6‑3. Si se tapa el orificio superior antes de sumergirlo, este quedará
saturado de aire que ocupa espacio, y por ende, no puede ser desplazado por el
agua, siempre y cuando la columna de agua no genere una presión superior a la de
la atmósfera.
Pesando globos inflados y la fuerza boyante
Ingenuamente se podría pensar que para
demostrar que el aire pesa, un observador moderno solo tiene que tomar dos
globos, uno colapsado, y otro inflado con el aire de sus pulmones, y luego
pesarlos usando una balanza analítica. Pero la cosa es un poco más complicada
que eso debido a la fuerza boyante. Para medir la masa debemos medir su peso,
que es una fuerza resultante de la gravitación de la tierra sobre esa masa y
hacer la conversión apropiada, pero eso solo funciona si la densidad del fluido
que rodea al objeto a medir es despreciable con respecto al objeto medido, y si
bien es evidente que los cuerpos sólidos son mucho más densos que el aire, un
globo de aire tiene una densidad semejante, y por ende la fuerza boyante
desviará los cálculos que se hagan de manera significativa.
Figura 6‑4. Comparar el peso de globos inflados y desinflados es una
estrategia para determinar que el aire tiene un peso asociado.
En el contexto griego la cosa era más
difícil ya que un simple globo es una pieza de tecnología moderna, pero ellos
ya intuían la posibilidad de medir la masa del aire ¿Cómo lo hicieron ellos?
Aristóteles describe otro experimento, con una vejiga inflada, en el que se
basó su creencia en el peso del aire en De Caelo [Sobre los cielos]
Libro IV.4:
“La tierra, entonces, y los cuerpos en
los que predomina la tierra, deben tener peso en todas partes, mientras que el
agua es pesada en cualquier lugar menos en la tierra, y el aire es pesado
cuando no está en el agua o en la tierra. En su propio lugar, cada uno de estos
cuerpos tiene peso excepto el fuego. , incluso aire. De esto tenemos evidencia
en el hecho de que una vejiga cuando está inflada pesa más que cuando está
vacía.”
El punto de vista de Aristóteles fue más o
menos aceptado durante la Edad Media. Pero este podría haber sido un caso de
creer lo correcto por las razones equivocadas, un ejemplo histórico de lo que
ahora se llama el problema del conocimiento de Gettier. Galileo se mostró
escéptico:
"Me inclino a creer que el aumento
de peso observado en la botella de cuero o en la vejiga no se debe a la
gravedad del aire, sino a los muchos vapores espesos mezclados con él en estas
regiones inferiores. A esto atribuiría el aumento de peso en la botella de
cuero ".
Como veremos más adelante el aire posee un
contenido de agua llamado humedad, por lo que Galileo distingue la humedad que
puede condensarse en un líquido del aire en si mismo que no se condensa. Esto
aplica a nuestros pulmones, ya que el aire de los pulmones humanos se mezcla
con agua en nuestro interior a través del moco y la sangre, por ende, el
experimento con los globos tendría el mismo problema mencionado por Galileo, si
lo inflamos con nuestros pulmones, lo que estaríamos introduciendo es aire
húmedo desoxigenado. Adicionalmente existe otro problema con el experimento de
los globos y es la boyancia o fuerza boyante.
Algunos de nosotros hemos tratado de
sumergir una bola de playa en el agua y sentimos como el agua la empuja
nuevamente hacia arriba. A esta fuerza se le llama Fuerza Boyante y todos los
líquidos aplican esta fuerza a todo objeto que es sumergido en estos. La Fuerza
Boyante existe porque la presión del fluido es más alta a mayor profundidad. El
problema es que el aire también ejerce fuerza boyante sobre el globo inflado y
por ende una balanza analítica es incapaz de registrar la ganancia en masa de
aire real, más allá del vapor de agua que ingrese y se condense.
La solución a estos problemas escapó a los
intentos de Galileo, posiblemente debido a que mucho de su tiempo estuvo
enfrascado con su conflicto con la iglesia católica y las autoridades civiles
sobre la posición de la Tierra y el Sol, por lo que la solución del peso del
aire quedó en manos de su alumno, Evangelista Torricelli.
El barómetro de Torricelli
En el siglo XVII, muchos científicos y
filósofos creían que la atmósfera no tenía peso. Evangelista Torricelli
(1608-1647), estudiante de Galileo, demostró que esto era falso. Inventó el
barómetro, que está hecho de un tubo de vidrio de más de 760 mm de largo que
está cerrado en un extremo, completamente lleno de mercurio e invertido en un
plato de mercurio. (Se debe tener cuidado de que no entre aire en el tubo, ni
entrar en contacto con el mercurio porque es altamente tóxico).
Figura 6‑5. El barómetro de mercurio.
Cuando el tubo se invierte en el plato,
parte del mercurio sale del tubo, pero queda una columna de mercurio en el
tubo. Torricelli argumentó que la superficie de mercurio en el plato
experimenta toda la fuerza de la atmósfera terrestre, que empuja el mercurio
hacia arriba por el tubo hasta que la presión ejercida por la columna de
mercurio hacia abajo, debido a la gravedad, es igual a la presión atmosférica
en la base del tubo. Por lo tanto, la altura, h, de la columna de mercurio es
una medida de la presión atmosférica y cambia a medida que cambia la presión
atmosférica.
Aunque la explicación de Torricelli encontró
una feroz oposición, también tuvo partidarios. Blaise Pascal, por ejemplo, hizo
que llevaran uno de los barómetros de Torricelli a la cima de una montaña y
comparó su lectura allí con la lectura de un barómetro duplicado en la base de
la montaña. A medida que se elevaba el barómetro, la altura de la columna de
mercurio disminuía, como se esperaba, porque la cantidad de atmósfera que
presionaba el mercurio en el plato disminuía a medida que el instrumento se
elevaba. Estos y otros experimentos finalmente prevalecieron, y se aceptó la
idea de que la atmósfera tiene peso, por ende, una masa, es decir el aire es un
algo que existe una entidad física medible, aunque no podamos verla.
En la siguiente demostración veremos como
el concepto de presión se deriva directamente de mediciones físicas empleando
conceptos Newtonianos como fuerza y aceleración:
🔎 DEMOSTRACION Demuestre
el funcionamiento de un Barómetro de Torricelli a partir de la ley de la
conservación de la masa.
En la demostración anterior, por lo tanto,
emergen ecuaciones clave del barómetro de Torricelli:
Con
las que podemos resolver problemas inversos.
Química
la ciencia central 13
✔ Muestra 10.01. Torricelli usó mercurio en su barómetro porque tiene una densidad
muy alta, lo que permite hacer un barómetro más compacto que uno basado en un
fluido menos denso. Calcule la densidad del mercurio, utilizando la observación
de que la columna de mercurio tiene 760 mm de altura cuando la presión
atmosférica es 1.01 x 105 Pa. Suponga que el tubo que contiene el
mercurio es un cilindro con un área de sección transversal constante.
✔ Muestra 10.01.1. ¿Cuál sería la altura de la columna si la presión externa fuera de 101
kPa y se usara agua (densidad = 1.00 g/cm3) en lugar de mercurio?
(a) 0.0558 m, (b) 0.760 m, (c) 1.03 x 104 m, (d) 10.3 m, (e) 0.103 m.
✔ Muestra
10.01.2. El galio se funde justo por encima de la temperatura ambiente y es
líquido en un rango de temperatura muy amplio (30–2204 °C), lo que significa
que sería un fluido adecuado para un barómetro de alta temperatura. Dada su
densidad, (6.0 g/cm3), ¿cuál sería la altura de la columna si se usa
galio como fluido barómetro y la presión externa es 9.5 x 104 Pa?
✔ Ejercicio 10.17b. ¿Cuál es la presión, en atmósferas, sobre el
cuerpo de un buzo si él o ella está a 39 pies por debajo de la superficie del
agua cuando la presión atmosférica en la superficie es de 0.97 atm?
✔ Ejercicio 10.18. El compuesto 1-yodododecano es un líquido no volátil con una densidad de 1.20 g/mL. La densidad del mercurio es 13.6 g/mL. ¿Qué predice para la altura de la columna de un barómetro basado en 1-yodododecano, cuando la presión atmosférica es de 749 torr?
El peso del aire
Aunque las ecuaciones anteriores
aparentemente sólo nos permiten hallar la presión de mercurio y la presión de
la atmósfera, como vimos en su proceso de demostración, estas presiones están
vinculadas a las masas, lo anterior implica que la masa de la columna de
mercurio debe ser necesariamente igual a la masa de la columna de aire que
se encuentra enfrentándola en el punto de equilibrio, por ende, el peso del
aire será igual al peso de esa columna de mercurio, pero a diferencia del
aire, sí podemos pesar la columna de mercurio, siempre y cuando contemos
con una medida del volumen que se encuentra al interior de la columna,
empleando la definición de densidad.
El manómetro
El barómetro permite determinar el peso
por unidad de área de toda la columna atmosférica sobre la que se encuentra el
plato de mercurio, pero aún nos queda el problema de pesar una muestra de gas,
como el aire, sin que la boyancia del resto de la atmosfera anule su peso. Para
resolver esto se emplea un instrumento semejante al barómetro, denominado el
manómetro.
Un manómetro es un dispositivo para medir
presiones. Un manómetro simple común consiste en un tubo de vidrio en forma de
U lleno de un poco de líquido. Normalmente, el líquido es mercurio debido a su
alta densidad. Si ambos extremos del tubo están abiertos entonces la altura de
ambas columnas es la misma, eso se debe a que la presión atmosférica está
ejerciendo un impacto igual en ambos lados. Sin embargo, si la presión del gas
en el tubo cerrado aumenta este puede empujar la columna opuesta, lo cual demostraría
que la presión interna es superior a la presión atmosférica.
Figura 6‑6. Modelos generales de manómetros simples.
Figura 6‑7. Modelos generales
de un manómetro ideal.
En 1661, el físico y astrónomo holandés
Christian Huygens inventó el manómetro de tubo en U, que era una modificación
del barómetro de Torricelli para determinar las diferencias de presión de gas.
La idea se fundamenta en el hecho de que, si conocemos la presión de la
atmosfera en un punto de equilibrio con la ayuda de dos columnas de mercurio,
es posible determinar la presión del gas incógnita para que el punto de
equilibrio se mantenga, en esencia es como si estuviéramos modelando una
balanza, pero en lugar de que se conserve la masa, lo que se conserva es la
presión. Idealmente una vez que se convierte la presión a peso empleando la
mecánica newtoniana, es posible obtener una medida del peso de un gas que no esté
afectada por la boyancia atmosférica como si sucede con el intento ingenuo de
pesar dos globos de aire. El problema es que una vez que se tuvo este
instrumento, se dieron cuenta que la altura de la columna podía variar en
función de la temperatura, por lo que hallar la masa del gas sin que fuera
afectado por la boyancia, seguía siendo un problema.
🔎
DEMOSTRACION. Demuestre el funcionamiento de un manómetro a partir del modelo
matemático del barómetro de Torricelli.
En la demostración anterior, por lo tanto,
emergen ecuaciones clave para el manómetro:
En ocasiones podemos tener situaciones
especiales, por ejemplo.
🔎
DEMOSTRACION. Como
calcular la altura del brazo abierto de un manómetro con la suma de alturas y
la diferencia de alturas.
|
Con las que podemos resolver problemas
inversos.
Química
la ciencia central 13
✔ Práctica
10.02.1. Si el gas dentro del matraz en el ejercicio
anterior se enfría de modo que su presión se reduzca a un valor de 715.7 torr,
¿cuál será la altura del mercurio en el brazo abierto? (Sugerencia: la suma de las
alturas en ambos brazos debe permanecer constante independientemente del cambio
de presión). (a) 49.0 mm, (b) 95.6 mm, (c) 144.6 mm, (d) 120.1 mm.
✔ Práctica
10.02.2. Si se aumentara la presión del gas dentro
del matraz y la altura de la columna en el brazo de extremo abierto aumentara
5.0 mm, ¿cuál sería la nueva presión del gas en el matraz, en torr?
✔ Ejercicio 10.17a. ¿Qué altura en metros debe tener una columna
de agua para ejercer una presión igual a la de una columna de mercurio de 760
mm? La densidad del agua es de 1.0 g/mL, mientras que la del mercurio es de
13.6 g/mL.
✔ Ejercicio 10.23a. Si la presión atmosférica es de 0.995 atm,
¿cuál es la presión del gas encerrado si la diferencia de niveles de mer curio
(h) es de 52 cm?
✔ Ejercicio 10.23b. Si la presión atmosférica es de 0.995 atm,
¿cuál es la presión del gas encerrado si la diferencia de niveles de mer curio
(h) es de 67 cm?
✔ Ejercicio 10.23c. Si la presión atmosférica es de 0.995 atm,
¿cuál es la presión del gas encerrado si la diferencia de niveles de mer curio
(h) es de 10.3 cm?
✔ Ejercicio 10.24a. Un manómetro de extremo abierto que contiene
mercurio está conectado a un recipiente de gas, como se muestra en el ejercicio
de muestra 10.2. ¿Cuál es la presión del gas encerrado en torr en cada una de
las siguientes situaciones? El mercurio en el brazo unido al gas es 15.4 mm más
alto que en el abierto a la atmósfera; la presión atmosférica es de 0.985 atm.
✔ Ejercicio 10.24b. Un manómetro de extremo abierto que contiene mercurio está conectado a un recipiente de gas, como se muestra en el ejercicio de muestra 10.2. ¿Cuál es la presión del gas encerrado en torr en cada una de las siguientes situaciones? El mercurio en el brazo unido al gas es 12.3 mm más bajo que en el abierto a la atmósfera; la presión atmosférica es de 0.99 atm.
Hallar el peso del gas es un poco más
complicado, ya que, a diferencia del barómetro, la medida de un manómetro no
solo está condicionada por la presión de la atmósfera y la presión del gas en
el contenedor, los científicos se dieron cuenta rápidamente que los cambios en
la temperatura afectaban la dilatación del gas en el interior del recipiente,
por lo que hallar el peso de un gas, sin que este se encuentre afectado por la
fuerza boyante es algo un poco más complejo.
La presión de la atmósfera
La fórmula que usamos para modelar el
barómetro de Torricelli nos permitiría, en el papel, calcular la densidad de la
columna de aire, empleando la densidad conocida del mercurio, el problema es
que esa densidad de aire sería en realidad la densidad promedio del aire en la
columna sobre el barómetro, desde donde se mide hasta el final de la atmósfera.
Sin embargo, como cualquier montañista
sabe, la densidad del aire y su contenido de oxígeno disminuyen rápidamente a
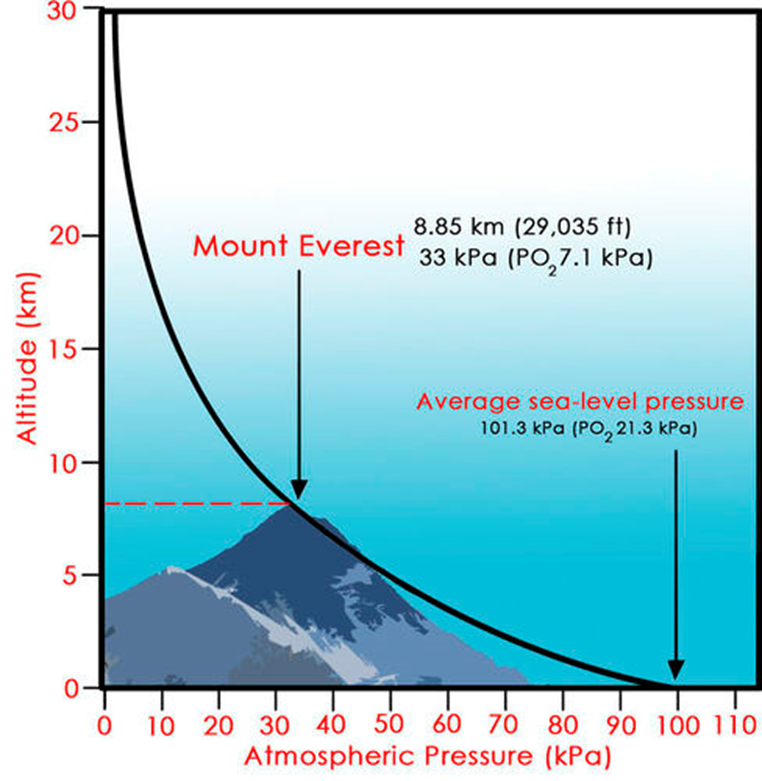
medida que aumentamos la altitud. De hecho, en una gráfica de altitud contra
presión atmosférica obtendremos que:
Figura 6‑8. Altitud en función de la presión atmosférica.
La altitud se relaciona con la presión de
la atmósfera por medio de una curva inversa, de forma tal que, a menor altitud,
la presión de la atmósfera es mayor, y viceversa, en términos de un valor
acumulativo que es superior a una línea recta, en otras palabras, la mayor
parte de la atmósfera de la Tierra se encuentra cerca del nivel del mar, y esta
disminuye rápidamente con solo elevarnos a una distancia relativamente baja,
aunque la atmosfera como tal sea comparativamente más alta.
Figura 6‑9. Aunque normalmente se nos dice que los gases se expanden
homogéneamente en un contenedor, esto no es cierto para contenedores de alturas
elevadas frente a una fuente de gravedad que atrae las partículas, la atmosfera
por lo tanto es heterogénea en su distribución, siendo más densa en el nivel
del mar.
Las personas, los cocos y las moléculas
del aire experimentan una fuerza gravitacional atractiva que los empuja hacia
el centro de la Tierra. Cuando un coco se suelta de un árbol, por ejemplo, esta
fuerza hace que el coco se acelere hacia la Tierra, aumentando su velocidad a
medida que su energía potencial se convierte en energía cinética.
Los átomos y moléculas de gas de la
atmósfera también experimentan una aceleración gravitacional. Sin embargo,
debido a que estas partículas tienen masas tan pequeñas, sus energías térmicas
de movimiento (sus energías cinéticas) anulan las fuerzas gravitacionales
parcialmente. Algunas partículas, las que acumulan más energía pueden vibrar a
gran altitud sin que la aceleración gravitacional las afecte
significativamente, pero aquellas moléculas que pierden calor o no se calientan
caen hasta la superficie del mar.
Los datos que emergen de un barómetro nos
permiten concluir que la mayoría de las moléculas de aire vibran con baja
energía a nivel del mar, hasta que logran calentarse y elevarse, pero muy pocas
lograran elevarse hasta llegar al límite superior de la atmósfera.
Definición moderna
Actualmente definimos la presión de un gas
como la suma promedio de los choques de las partículas del gas contra las
paredes de su contenedor. Cuando golpean las paredes de un contenedor, ejercen
presión. Si calentamos el contenedor, las moléculas se mueven más rápido y se
estrellan contra las paredes más a menudo y con mayor fuerza, lo que aumenta la
presión. Las partículas de gas en el aire, principalmente oxígeno y nitrógeno,
ejercen una presión sobre nosotros llamada presión atmosférica. A medida que
vas a altitudes mayores, la presión atmosférica es menor porque hay menos
partículas en el aire, lo cual incluye menos oxígeno, por lo que se hace más
difícil respirar.
Unidades
Las unidades de la variable presión son
problemáticas debido a su gran diversidad, las unidades más comunes utilizadas
para la medición de la presión del gas son la atmósfera (atm) y milímetros de
mercurio (mmHg) al ser las primeras que empleó Torricelli. En el informe
meteorológico de TV, es posible que escuches o veas la presión atmosférica en pulgadas
de mercurio o kilopascales (kPa) en países distintos de los Estados Unidos. En
un hospital, se puede usar la unidad torricelli (torr) o libras por pulgada
cuadrada (psi).
✔ Ejemplo. Convertir
los siguientes datos de presión a atmósferas: 2.026 bar; 303 955 Pa; 1140 mmHg
Química
de Chang 10
✔ Práctica
5.1. Convertir 749 mmHg a atmósferas
✔ Ejemplo 5.2.
La presión atmosférica en San Francisco en un día determinado fue de
732 mmHg. ¿Cuál fue la presión en kPa?
✔ Práctica
5.2. Convertir 295 mmHg a kilopascales
✔ Problema-5.13.
Convierta 562 mmHg en atm
✔ Problema-5.14. La presión atmosférica en la cima del monte McKinley es de 606 mmHg
en un día determinado. ¿Cuál es la
presión en atm y en kPa?
Química La ciencia Central 11
✔ 10.1.a. Convertir 0.357 atm a torr.
✔ 10.1.b. Convertir 6.6 x 10-2 torr en atm.
✔ 10.1.c. Convertir 147.2 kPa a Torr.
✔ Práctica 10.01. En países que utilizan el sistema métrico, como Canadá, la presión
atmosférica en los informes meteorológicos se da en unidades de kPa. Convierta
una presión de 745 Torr en kPa.
✔ Práctica 10.01b. Una unidad inglesa de presión que a veces se usa en ingeniería es
libras por pulgada cuadrada (lb/in2), o psi: 1 atm = 14.7 lb/in2.
Si una presión se informa como 91.5 psi, exprese la medida en atmósfera.
Química La ciencia Central 13
✔ Ejercicio 10.19a. La presión atmosférica típica en la cima del monte Everest (29 028
pies) es de aproximadamente 265 torr. Convierta esta presión a atm.
✔
Ejercicio 10.19bc. La presión atmosférica
típica en la cima del monte Everest (29 028 pies) es de aproximadamente 265
torr. Convierta esta presión a mmHg y
pascales
✔
Ejercicio 10.19d. La presión atmosférica típica en la cima del monte Everest (29 028
pies) es de aproximadamente 265 torr. Convierta esta presión a bars
✔
Ejercicio 10.19e. La presión atmosférica típica en la cima del monte Everest (29 028
pies) es de aproximadamente 265 torr. Convierta esta presión a psi
✔ Ejercicio 10.20a. Convertir 0.912 atm a torr,
✔
Ejercicio 10.20b. Convertir 0.685 bar a kilopascales
✔
Ejercicio 10.20c. Convertir 655 mm Hg a atmósferas
✔
Ejercicio 10.20d. Convertir 1.323 x 105 Pa a atmósfera
✔
Ejercicio 10.21a. En los Estados Unidos, las
presiones barométricas generalmente se expresan en pulgadas de mercurio (in.
Hg). En un hermoso día de verano en Chicago, la presión barométrica es de 30.45
pulgadas Hg. Convierta esta presión a torr.
✔
Ejercicio 10.21b. En los Estados Unidos, las
presiones barométricas generalmente se expresan en pulgadas de mercurio (in.
Hg). En un hermoso día de verano en Chicago, la presión barométrica es de 30.45
pulgadas Hg. Convierta esta presión a atm.
✔
Ejercicio 10.22a. El huracán Wilma de 2005 es el
huracán más intenso registrado en la cuenca del Atlántico, con una lectura de
baja presión de 882 mbar (milibares). Convierta esta lectura en atmósferas.
✔
Ejercicio 10.22b. El huracán Wilma de 2005 es el
huracán más intenso registrado en la cuenca del Atlántico, con una lectura de
baja presión de 882 mbar (milibares). Convierta esta lectura en torr.
✔ Ejercicio 10.22c. El huracán Wilma de 2005 es el huracán más intenso registrado en la cuenca del Atlántico, con una lectura de baja presión de 882 mbar (milibares). Convierta esta lectura en pulgadas de Hg.
La presión sanguínea
La presión arterial se mide con un
dispositivo llamado esfigmomanómetro (del griego sphygmos = “pulso”). Consiste
en un manguito inflable para restringir el flujo sanguíneo, un manómetro para
medir la presión y un método para determinar cuándo comienza el flujo sanguíneo
y cuándo se impide. Desde su invención en 1881, ha sido un dispositivo médico
esencial. Hay muchos tipos de esfigmomanómetros: manuales que requieren un
estetoscopio y son utilizados por profesionales médicos; los de mercurio,
usados cuando se requiere la mayor precisión; mecánicos menos precisos; y
digitales que se pueden utilizar con poca formación pero que tienen
limitaciones. Cuando se usa un esfigmomanómetro, el manguito se coloca
alrededor de la parte superior del brazo y se infla hasta que el flujo de
sangre se bloquea por completo, luego se suelta lentamente. A medida que late
el corazón, la sangre forzada a través de las arterias provoca un aumento de la
presión. Este aumento de presión en el que comienza el flujo sanguíneo es la
presión sistólica, la presión máxima en el ciclo cardíaco. Cuando la presión
del manguito es igual a la presión sistólica arterial, la sangre fluye más allá
del manguito, creando sonidos audibles que se pueden escuchar con un
estetoscopio. A esto le sigue una disminución de la presión a medida que los
ventrículos del corazón se preparan para otro latido. A medida que la presión
del manguito continúa disminuyendo, eventualmente ya no se escucha el sonido;
esta es la presión diastólica, la presión más baja (fase de reposo) en el ciclo
cardíaco. Las unidades de presión arterial de un esfigmomanómetro están
expresadas en milímetros de mercurio (mmHg).
La presión atmosférica a gran escala
A lo largo de los siglos, la gente ha
observado las nubes, los vientos y las precipitaciones, tratando de discernir
patrones y hacer predicciones: cuándo es mejor plantar y cosechar; si es seguro
emprender un viaje por mar; y mucho más. Ahora enfrentamos desafíos complejos
relacionados con el clima y la atmósfera que tendrán un gran impacto en nuestra
civilización y el ecosistema. Varias disciplinas científicas diferentes
utilizan principios químicos para ayudarnos a comprender mejor el tiempo, la
atmósfera y el clima. Estos son la meteorología, la climatología y la ciencia
atmosférica. La meteorología es el estudio de la atmósfera, los fenómenos
atmosféricos y los efectos atmosféricos en el clima de la Tierra. Los
meteorólogos buscan comprender y predecir el clima a corto plazo, lo que puede
salvar vidas y beneficiar la economía. Los pronósticos meteorológicos son el
resultado de miles de mediciones de presión atmosférica, temperatura y
similares, que se compilan, modelan y analizan en centros meteorológicos de
todo el mundo.
En cuanto al clima, los sistemas de baja
presión ocurren cuando la presión atmosférica en la superficie de la tierra es
más baja que la del entorno circundante: el aire húmedo se eleva y se condensa,
produciendo nubes. El movimiento de la humedad y el aire dentro de varios
frentes meteorológicos provoca la mayoría de los fenómenos meteorológicos.
Un frente de baja presión de humedad sobre
el océano genera un efecto de esponja o jeringa sobre el agua, formando nubes a
gran velocidad en un sistema cíclico que puede terminar en trombas marinas,
tormentas o huracanes/tifones con un poder energético comparable únicamente al
de las bombas nucleares.













No hay comentarios:
Publicar un comentario